Velocity is the rate of displacement of an object. It is measured in m/s. Acceleration is the rate of change of velocity of an object. It is measured in m/s2. They are both vector quantities i.e. both magnitude and direction are required to fully specify them.
Comparison chart
Defining Velocity and Acceleration
Velocity is the change in position (location) of an object per unit time. e.g., a bus traveling at a velocity of 60 miles per hour from North to South. The SI unit of velocity is meters per second (m/s). In general, it is important to indicate the direction of motion when specifying the velocity. In other words, it is a vector quantity, as opposed to a scalar quantity that would specify the speed without mentioning the direction.
Acceleration is the change in velocity of an object per unit time. The SI unit of acceleration is meters per second per second i.e., meters per second squared (m/s2). e.g., the acceleration of a free-falling object on Earth is 9.8 m/s2 because of Earth's gravity.
Calculating velocity
Velocity is the distance an object has moved in a particular direction within a specified time interval. If the object returns to its starting position then the velocity is zero.

This video explains how to calculate average velocity over a constant acceleration:
Calculating acceleration
Instantaneous acceleration is the change in velocity  divided by the duration of the interval dt:
divided by the duration of the interval dt:
 i.e. the derivative of the velocity vector as a function of time.
i.e. the derivative of the velocity vector as a function of time.
Average acceleration over a period of time is the change in velocity ( ) divided by the duration of the period (Δt)
) divided by the duration of the period (Δt)
Therefore the SI unit of acceleration is meter per second per second, i.e. meter per second squared (m/s2).
This video explains how to calculate acceleration using the example of a Porsche.
Types of Acceleration
If an object is moving at constant speed in a circular motion -- such as a satellite orbiting the earth -- it is said to be accelerating because change in direction of motion means its velocity is changing even if speed may be constant. (See Speed vs Velocity) This is called centripetal (directed towards the center) acceleration. On the other hand, if the direction of motion of the object is not changing but its speed is, this is called tangential acceleration.
If the direction of acceleration is in the same direction as that of velocity then the object is said to be speeding up or accelerating. If the acceleration and velocity are in opposite directions then the object is said to be slowing down or decelerating.
An example of constant acceleration is the effect of the gravity of earth on an object in free fall.
Velocity and Acceleration in a Pendulum
When a pendulum swings from side to side, its velocity and acceleration vary — both in magnitude and in direction — at each point during the motion.
The magnitude of velocity of a pendulum is highest in the center and lowest at the edges. On the other hand, the magnitude of its acceleration is highest at the edges and lowest at the center.
Practical applications
- Applications of velocity in real life are to calculate the time taken for a storm to reach the coastline, the time taken for a satellite to reach moon and so on.
- Accelerometers are used to measure acceleration of an object. Measurement of acceleration of a vehicle enables to evaluate overall vehicle performance and response.
- Detection of rapid negative acceleration of a vehicle is used to detect vehicle collision and deploy airbags.
- The measurement of acceleration is also used to measure seismic activity, inclination and machine vibration.
- Vibration monitoring is used in industries such as automotive manufacturing, machine tool applications, pharmaceutical production, power generation and power plants, pulp and paper, sugar mills, food and beverage production, water and wastewater, hydropower, petrochemical and steel manufacturing.


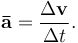


 Speed
Speed  Centrifugal Force
Centrifugal Force  Kinetic and Potential Energy
Kinetic and Potential Energy Difference Between Mass and Weight
Difference Between Mass and Weight Current
Current  Electric Field
Electric Field
Comments: Acceleration vs Velocity